healthforinsure.com reviews đến các em học sinh lớp 10 nội dung bài viết Chứng minh bất đẳng thức bằng cách sử dụng phép biến hóa tương đương, nhằm mục đích giúp các em học giỏi chương trình Toán 10.
Bạn đang xem: Chứng minh các bất đẳng thức



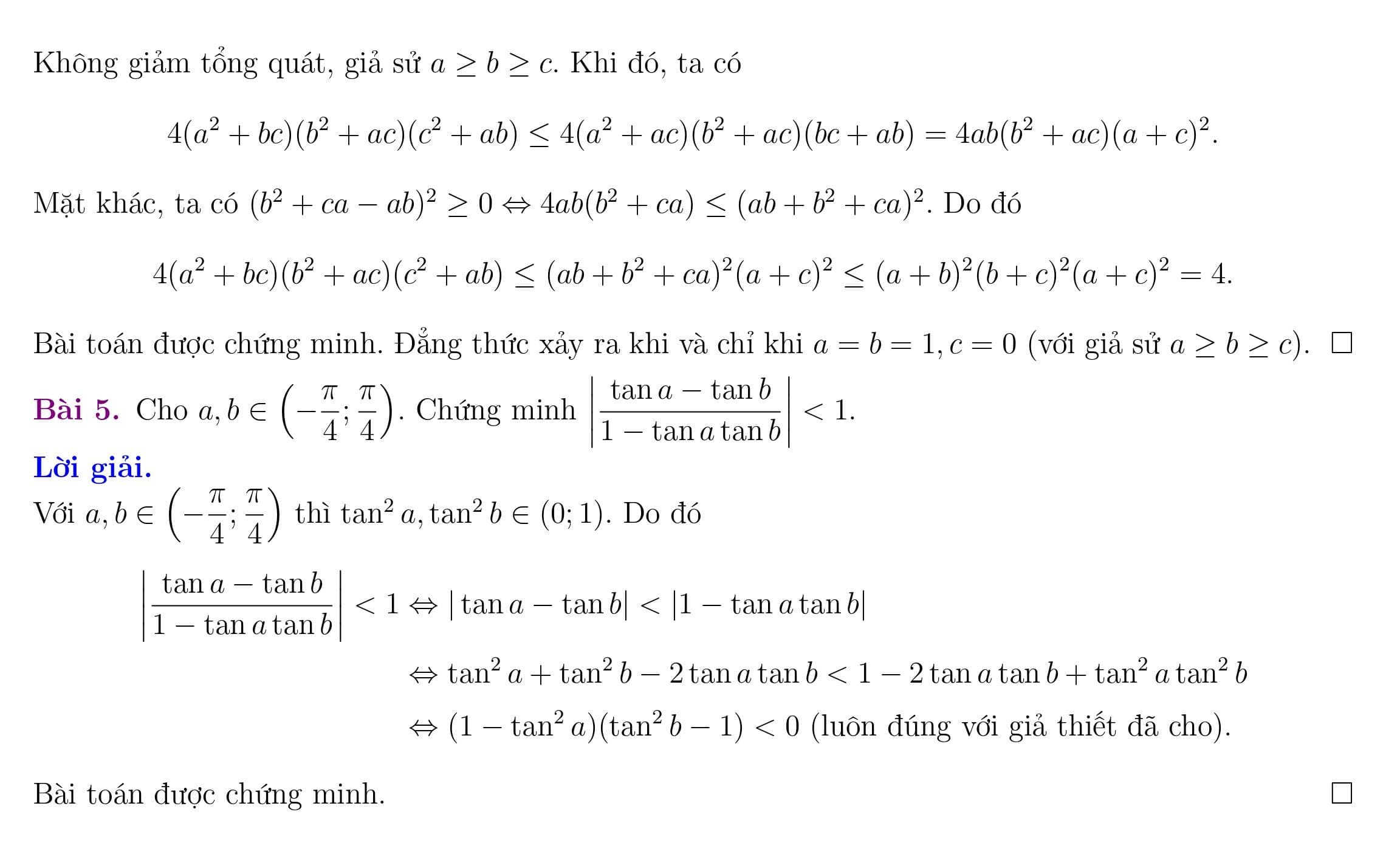
Nội dung bài viết Chứng minh bất đẳng thức bằng cách sử dụng phép biến hóa tương đương:Sử dụng phép chuyển đổi tương đương. Để chứng minh một bất đẳng thức ta hoàn toàn có thể sử dụng các cách sau: biến đổi bất đẳng thức cần minh chứng tương đương với 1 bất đẳng thức đang biết. áp dụng một bất đẳng thức đã biết, thay đổi để dẫn đến bất đẳng thức đề xuất chứng minh. Một vài bất đẳng thức thông dụng. BÀI TẬP DẠNG 1. Lấy ví dụ như 1. Chứng minh √1 − x + √x + 2 ≤ √6, ∀x ∈ <−2; 1>. Bất đẳng thức cuối luôn luôn đúng. Vậy, việc được chứng minh. Ví dụ 2. Chứng tỏ a2 + b2 + 2 ≥ 2(a + b), với tất cả số thực a, b. Lời giải. Với tất cả số thực a, b ta luôn luôn có(a − 1)2 + (b − 1)2 ≥ 0 ⇔ a2 + b2 + 2 ≥ 2(a + b). Câu hỏi đã được triệu chứng minh. Đẳng thức xẩy ra khi còn chỉ khi a = b = 1.Ví dụ 3. Cho các số thực x, y, z. Chứng tỏ các bất đẳng thức sau: Bất đẳng thức cuối phân biệt đúng. Đẳng thức xẩy ra khi và chỉ khi x = y = z. Phép minh chứng hoàn tất. Đẳng thức đã đạt được khi và chỉ khi x = y = 1. Vấn đề đã được hội chứng minh. Lấy một ví dụ 4. Chứng minh các bất đẳng thức sau: Bất đẳng thức này luôn đúng với mọi a, b không âm. Đẳng thức xẩy ra khi và chỉ khi a = b. Chuyển đổi bất đẳng thức đã cho tương đương với (a − b)2 (a2 − ab + b2) ≥ 0 (hiển nhiên đúng). Đẳng thức xảy ra khi và chỉ khi a = b. Ví dụ 5. Mang đến a, b là các số thực thỏa mãn nhu cầu ab ≥ 1. Chứng minh. Bất đẳng thức cuối luôn đúng với tất cả a, b thỏa mãn nhu cầu ab ≥ 1. Đẳng thức xảy ra khi và chỉ còn khi ab = 1 hoặc a = b. Lấy ví dụ như 6. đến x, y, z là các số thực dương thỏa mãn. Vậy, vấn đề được bệnh minh. Đẳng thức dành được khi còn chỉ khi x = y = z.BÀI TẬP TỰ LUYỆN. Bài bác 1. Mang lại a, b, c là những số thực thỏa mãn a + b + c = 3. Chứng tỏ a4 + b4 + c4 ≥ a3 + b3 + c3. Lời giải. HD: Bất đẳng thức cần minh chứng tương đương cùng với 3(a4 + b4 + c4) ≥ (a + b + c)(a3 + b3 + c3). Thực hiện biến đổi tương đương quy về bất đẳng thức. Bài bác 2. Mang đến x, y, z là các số thực dương thỏa mãn xyz = 1. Chứng tỏ rằng với a, b, c dương cùng abc = 1. Bất đẳng thức đã đến trở thành. Câu hỏi được chứng minh. Đẳng thức xẩy ra khi còn chỉ khi x = y = z = 1. Bài xích 4. Mang đến a, b, c là những số thực không âm thỏa mãn nhu cầu (a + b)(b + c)(c + a) = 2. Chứng tỏ rằng (a2 + bc)(b2 + ac)(c2 + ab) ≤ 1. Không bớt tổng quát, mang sử a ≥ b ≥ c. Vấn đề được triệu chứng minh. Đẳng thức xảy ra khi còn chỉ khi a = b = 1, c = 0 (với giả sử a ≥ b ≥ c).
Danh mục Toán 10 Điều hướng bài xích viết
Giới thiệu
healthforinsure.com là website share kiến thức tiếp thu kiến thức miễn phí những môn học: Toán, trang bị lý, Hóa học, Sinh học, tiếng Anh, Ngữ Văn, kế hoạch sử, Địa lý, GDCD từ lớp 1 đi học 12.
Xem thêm: Cây Trầu Bà Cánh Phượng
Các bài viết trên healthforinsure.com được cửa hàng chúng tôi sưu trung bình từ mạng xã hội Facebook cùng Internet. healthforinsure.com không chịu trách nhiệm về các nội dung có trong bài xích viết.









